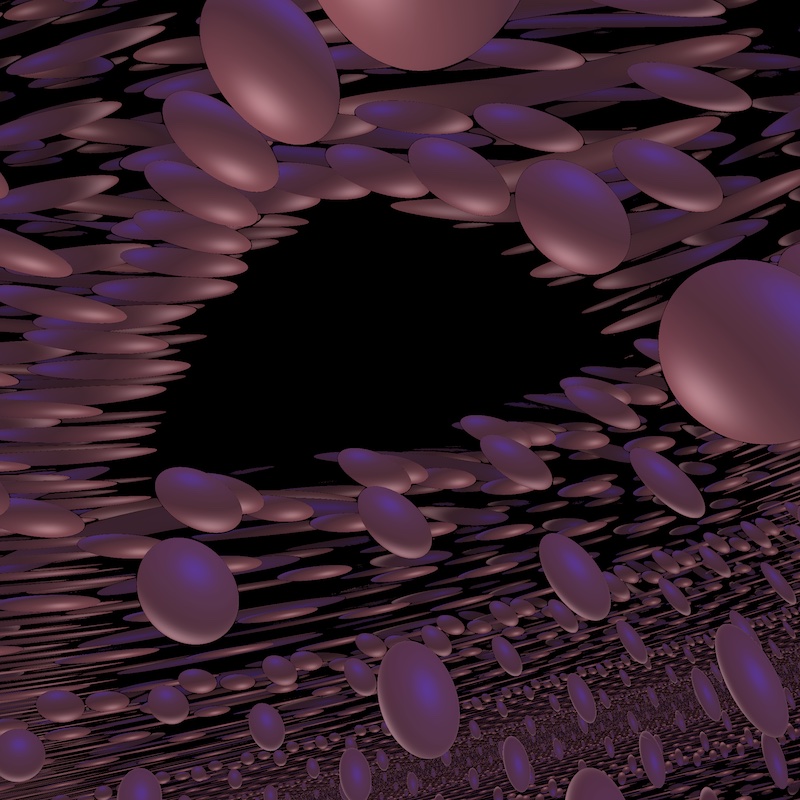
The Sol geometry
What is Sol?
Sol is a 3-dimensional solvable Lie group. It can also be seen as the universal cover of the suspension of a 2-torus by an Anosov matrix.
Click on the button below to reveal a concrete model of Sol.
As a set of points, Sol is the usual 3-dimensional space $X = \mathbb R^3$ with coordinates $(x,y,z)$. The riemanian metric on Sol is given by $$ ds^2 = e^{-2z} dx^2 + e^{2z}dy^2 + dz^2.$$
Consider to points $p_1 = (x_1, y_1, z_1)$ and $p_2 = (x_2, y_2, z_2)$ in $X$. The group law in Sol is given by $$ p_1 \ast p_2 = (x_1 + e^{z_1}x_2, y_1 + e^{-z_1}y_2, z_1 + z_2) $$ The left action of Sol on itself is an action by isometries. Sol has finite index in its isometry group. More precisely ${\rm Isom}(X) = X \rtimes \mathbb D_8$, where $\mathbb D_8$ is the dihedral group of order eight.
Some views of Sol
Warning: Some of the real-time simulations below requires a powerful graphic card. If your computer is not fast enough, you can reduce the size of your browser window. Click on the button below to reveal the fly commands.
The default controls to fly in the scene are the following. If you have a different keyboard, the keys should be the ones having the same location as the given ones on a QWERTY keyboard.
| Command | QWERTY keyboard | AZERTY keyboard |
|---|---|---|
| Yaw left | a | q |
| Yaw right | d | d |
| Pitch up | w | z |
| Pitch down | s | s |
| Roll left | q | a |
| Roll right | e | e |
| Move forward | arrow up | arrow up |
| Move backward | arrow down | arrow down |
| Move to the left | arrow left | arrow left |
| Move the the right | arrow right | arrow right |
| Move upwards | ' | ù |
| Move downwards | / | = |
HD pictures of Sol can be found in the gallery (in preparation)
Features of Sol
Some features of Sol are described in the following Bridges paper.