The eight Thurston geometries

From Euclid to Thurston… and beyond

Euclid and the parallel postulate

The Elements by Euclid, written around 300 BC, is one of the oldest complete treatise of ancient greek mathematics that we know. This book had a strong influence, in part because of its deductive treatment of mathematics. In particular Euclid states in the first book several postulates from which everything else should be deduced. While the first postulates are very “natural” (e.g. given any two points, there is a segment joining them) the fifth postulate, also known as the parallel postulate plays a different role.

The emergence of non-euclidean geometries

For a long time nobody doubt about the validity of the fifth postulate. Nevertheless, many mathematicians tried to deduce it from the previous ones… in vain. It was only during the 19th century that several mathematicians (Gauß, Bolyai, and Lobatchevski) independently realized that one can build “other geometries” where the first four postulate hold while the fifth one fails. This breakthrough demonstrates that the parallel postulate is not a consequence of other four. It led to the study of non-euclidean geometry.

Classifying geometric structures

Knowing that there exist several distinct geometries, a natural question is to classify all of them. In dimension two, the solution of this problem is given by the Uniformization Theorem. Roughly speaking, it states that any two-dimensional compact manifold can be endowed with a metric with constant curvature. If the curvature is positive (respectively zero, negative) then the geometry is modeled on the two-sphere (respectively the euclidean plane, the hyperbolic plane).

In dimension three, the situation is more complicated: a compact three-manifold does not always admit a geometric structure. However, the Geometrization Theorem, stated by Thurston and proved by Perelman, explains that any compact three-manifold can be cut along essential spheres and tori so that the interior of each resulting piece admits a geometric structure. There are eight possible geometric structures, called Thurston’s geometries.

This website allows you to experiment what it would be to live in each of them.

A first look at the Thurston geometries

The video below, displayed during the exhibition Seeing the unseen at the Wignall Museum of Contemporary Art presents various scenes in the eight Thurston geometries.

A few real time simulations

Warning: The simulations below are working real-time on your computer. They include numerous objects and shading effects requiring a powerful graphic card. If your computer is not fast enough, you can reduce the size of your browser window. You can also explore each geometry page to try less greedy simulations.

Euclidean

A collection of eight spheres in the 3-torus.

Spherical

A collection of eight spheres in the 3-torus.

Hyperbolic

A collection of twelve spheres in Seifert-Weber dodecahedral space.

$S^2 \times \mathbb E$

A collection of 20 spheres in the Hopf manifold $S^2 \times S^1$, arranged on the vertices of an icosahedron in the $S^2$ factor.

$\mathbb H^2 \times \mathbb E$

A collection of four spheres in the trivial circle bundle over a hyperbolic orbifold torus with cone angle $\pi$.

Nil

A collection of four spheres in a Dehn twist torus bundle.

$\widetilde{\rm SL}(2,\mathbb R)$

A collection of four spheres in the unit tangent bundle to a hyperbolic orbifold torus with cone angle $\pi$.

Sol

A collection of four spheres in an Anosov torus bundle.

The geometries

The euclidean space $\mathbb E^3$

The euclidean space corresponds to the “usual” 3D geometry we learn at school. It is the geometry of the flat real 3-dimensional vector space $\mathbb R^3$.

The spherical space $S^3$

The space $S^3$ is the 3-dimensional analogue of the usual sphere in 2 dimensions. It is an isotropic space (all the directions play the same role). Among the eight Thurston geometries, it is the only compact one. It can be seen as the unit tangent bundle of the 2-sphere. This point of view is also knwon as the Hopf fibration.

The hyperbolic space $\mathbb H^3$

The hyperbolic space $\mathbb H^3$ is the three-dimensional analog of the hyperbolic plane. It is an isotropic space (all the directions play the same role). Among the eight geometries, this is probably the one which has the richest class of lattices.

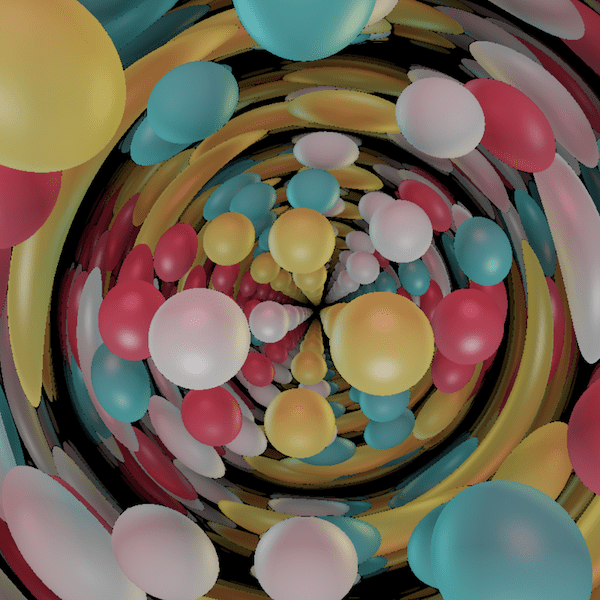
The product geometry $S^2 \times \mathbb E$

This geometry is the cartesian product of the two-sphere and the real line. It can be also seen as the universal cover of the product $M = S^2 \times S^1$ where $S^2$ is the two-sphere and $S^1$ the unit circle.

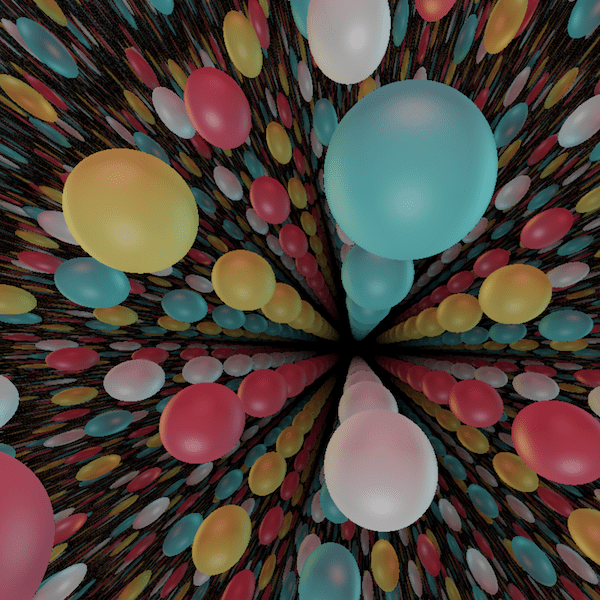
The product geometry $\mathbb H^2 \times \mathbb E$

This geometry is the cartesian product of the hyperbolic plane and the real line. It can be also seen as the universal cover of the product $M = \Sigma_g \times S^1$ where $\Sigma_g$ is a compact surface of genus $g \geq 2$ and $S^1$ the unit circle.

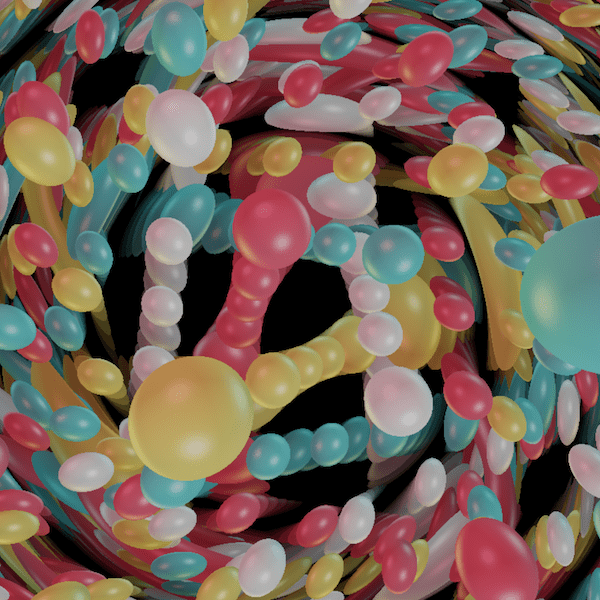
The Nil geometry

Nil is a 3-dimensional nilpotent Lie group. It can also be seen as the universal cover of the suspension of a 2-torus by a Dehn twist.

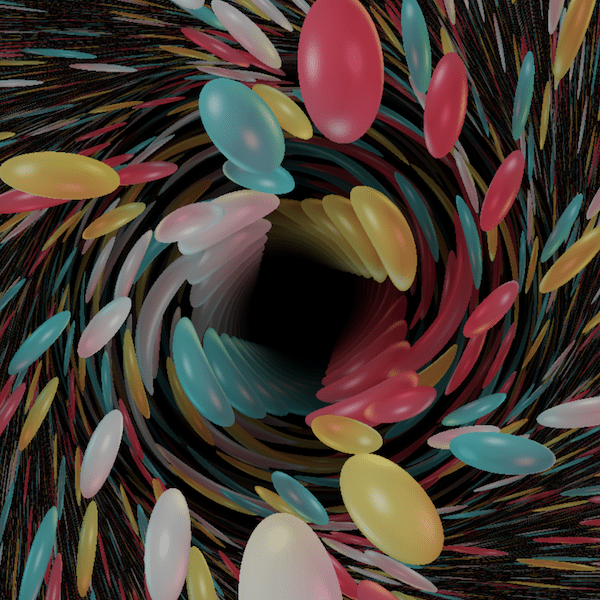
The universal cover of ${\rm SL}(2,\mathbb R)$

${\rm SL}(2,\mathbb R)$ is the set of all $2 \times 2$-real matrices with determinant one. The space $\widetilde{\rm SL}(2,\mathbb R)$ is its universal cover. There are several ways to think about this space. ${\rm SL}(2,\mathbb R)$ is for instance the unit tangent bundle of the hyperbolic plane $\mathbb H^2$. This point of view gives $\widetilde{\rm SL}(2,\mathbb R)$ a structure of a twisted metric line bundle over $\mathbb H^2$, which can be thought as a hyperbolic analogue of the Hopf fibration

The Sol geometry

Sol is a 3-dimensional solvable Lie group. It can also be seen as the universal cover of the suspension of a 2-torus by an Anosov matrix.